Hey everyone! It's me Shouq. This is the first lab report for an Industrial Engineering class called Operational research / optimization - OR1 - IE335 which I took in Fall 2017 in the American University of the Middle East (AUM) in Kuwait.
Abstract
The objective of this report is to show the
work in how to find the cost-minimizing pattern of assembly across three plants
that Ford Company has using the operational research method. First, an introduction
regarding the problem is provided with every detail regarding it. Then the
decision variables are identified as well as the objective functions and the
constraints of the problem. After that the final linear programming formulation
will be presented and explained. Also, the problem is solved using Excel solver
to find the answer of the linear programming problem. Finally, a sensitivity
report is presented as well as a what-if analysis.
Keywords: Ford, Plants,
problem, operational, research, sensitivity, what-if, analysis.
Introduction
A company called Ford has three different assembly plants that are
placed in different places all over the country. Plant number one is located in
the state of Ohio. The requirement to make one automobile in plant number one
is 2 hours of labor as well as a 1 hour of machine time. When it comes to plant
number 2, it is located in the state of California. It requires 1.5 hours of
labor and 1.5 hours of machine time in order to assemble one automobile.
Finally, planet number three is located in the state of Tennessee. It was built
in 1981. And in order to make one automobile in planet number 3, we will need
1.1 hours of labor and 2.5 of machine time as well. All of that is shown in
Table 1.
Labor per day
|
Machine time per day
|
|
Plant Number One
|
2 hours
|
1 hour
|
Plant Number Two
|
1.5 hours
|
1.5 hours
|
Plant Number Three
|
1.1 hours
|
2.5 hours
|
|
The company pays $30 for every hour of labor. It also pays $10 for
every hour of machine time per day to assemble one automobile. Every plant has
different capacity of machine work for every single day. When it comes to the
first plant, it has a daily capacity of 1,000 hour of machine time. On the
other hand, the second plant has a daily capacity of machine time that is equal
to 900 hours. And the highest daily capacity of machine time is in the third plant
that is equal to 2,000 hours. The manufacturer of Ford Company has a daily goal
of assembling 1,800 automobiles.
Problem formulation
Decision variables
·
X1: Number of automobile products that are
produced by plant number 1.
·
X2: Number of automobile products that are
produced by plant number 2.
·
X3: Number of automobile
products that are produced by plant number 3.
Objective function
Min Z = [[(30)(2)
+ (1)(10)] X1 + [(30)(1.5) + (10)(1.5)]
X2 + [(30)(1.1) + (10)(2.5)] X3]
Equation
1
For the objective function; it is minimization where
we minimize the pattern of assembly across three different plants. From
Equation 1 above, Z is the numbers of hours of labor multiplied by 30$ that is
the amount the company is paying for labor. Then adding it to the numbers of
hours of machine time multiply by $10 which is the amount the firm is willing
to pay for the machine time per hour with the number of product automobile by
the three different plants that we have. (Xi = 1, 2, 3)
Subject
to
·
X1 + X2 + X3 >= 1800
Equation 2
Equation 2 is the equation of the first constraint. We
will sum up the number of product automobile by plant 1, 2, and 3 as well. We
know that the sum of all Xi where i = 1, 2, 3 should be greater than or equal
to 1800. 1800 is the daily target of number of automobiles that the
manufacturer of Ford Company has.
·
0.5 X1
+ X1 =< 1000
Equation 3
Equation 3 is the equation of the second constraint.
It represents the number of automobile products that are produced
by plant number one that is X1. We divided
the number of labor with the number of machine times in plant number one and we
added them with the number of automobile products that
are produced by plant number 1 without
dividing.
·
(1.5 / 1.5) X2 + X2 =< 900
Equation 4
Equation 4 is the equation of the third constraint. It
represents the number of automobile products that are produced
by plant number two which is X2. We divided
the number of labor hours to the number of machine times that are required when
it comes to plant number two. Then we add it to the number of
automobile products that are produced by plant number 2. The amount of all of
that added together should be less than or equal to 900. 900 are the number of
hours that is the daily capacity of machine time in the second plant.
·
(1.1 / 2.5) X3 + X3 =< 2000
Equation 5
Equation 4 is the equation of the forth constraint. It
represents the number of automobile products that are produced
by plant number three which is X3.
We divided the number of labor hours to the number of machine times that are
required when it comes to planet number three. Then we added it all to the
number of automobile products that are produced by plant number three. The
amount of all of that added together should be less than or equal to 2000. 2000
is the number of hours that is the daily capacity of machine time in the second
plant.
·
X1, X2,
X3 >= 0
Equation 6
Equation
6 is considered to be a non-negativity constraint. For the values of X1, X2 and X3 are supposed to be
zero or a positive number that is greater than zero as it does not make sense
to produce negative numbers of products, so zero is considered to be the smallest
number for production which means producing no products. Also, it can be any
number that is more than zero.
Conclusion
The final Linear Programming Formulation is
Figure 1: Final LP
formulation
Methodology
First, we will start by providing
the Excel Solver solution of the previously mentioned LP formulation. Then we
will continue by finding and presenting the sensitivity analysis as well. Finally,
we will end it with the what-if analysis. In each part of the solutions we will
provide an explanation of what we did and how did we get that specific answer.
Excel
Figure2: The
table of the solution in Excel
As
showed in Figure 2, we defined the objective function (Z) that is minimizing the pattern of assembly across three different plants.
Z is the numbers of hours of labor multiplied by 30$ that is the amount the
company is paying for labor. Then adding it to the numbers of hours of machine
time multiply by $10 which is the amount the firm is willing to pay for the
machine time per hour with the number of product automobile by the three
different plants that we have. (Xi = 1, 2, 3)The first number in the third row is equal to 70, and
we got it by multiplying 30 by 2 ten adding it to 1 multiplied by 10. This all
was explained by details in the problem formulation part. The
final result of objective function is 105222 that got transformed to 411 when
we changed the decimal point of the answer to zero. The answer was found using Excel
solver. Moreover, we defined the constraints as c1, c2, c3, and c4. The first constraint is the sum of everything should
be greater than or equal to 1800. 1800 is the daily target of number of
automobiles that the manufacturer of Ford Company has. We got the final result of this constraint by using
Excel solver. The second constraint represents the number of
automobile products that are produced by plant number one. We got the final result of this constraint by using
Excel solver and it should be less than 1800. The third constraint represents the
number of automobile products that are produced by plant number two, and it should be less than 900. The forth constraint
represents the number of automobile products that are produced
by plant number three, and it should
be less than 2000. Finally, we used the Excel solver to get the values for the
constraints and the value of (Xi).
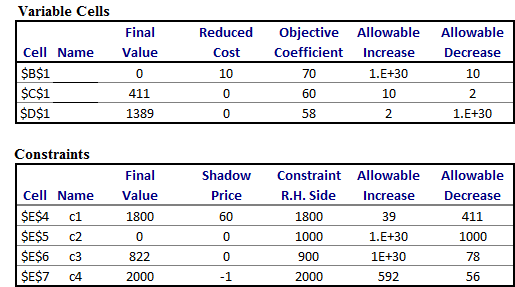
Sensitivity analysis
Figure 3: The
table sensitivity analysis
The optimal
solution of the earlier linear programming problem is to order zero automobile products that are produced by plant number one as well
as 411 automobile products that are produced by plant number two. Also, we get
to order 1389 automobile products that are produced by plant number three. The
solution mentioned above in Figure 3 has1800 that is daily goal of assembling
1,800 automobiles that is assigned by the manufacturer of Ford Company.
What-if analysis
What is the cost of assembling one
extra automobile given that the current output level of 1,800 automobiles?
Would the answer be different if the goal of the production was only 8,000
automobiles? Why or why not?
The answer will be
different if we changed the production target from 1,800 to 8,000 of the cost
of assembling one extra automobile will be equal to 6,200. Also, from the
previous data in Figure 2 we notice that 6,200 are out of range.
A team of production
specialists has indicated that the auto manufacturer can achieve efficiencies
at its Bakersfield plant by reconfiguring the assembly line. The
reconfiguration has the effect of increasing the productivity of the labor at
this plant from 1.5 hours to 1.2 hour per automobile. By how much will the
firm’s costs fall as a result of this change, assuming that it continues to
produce 1,800 automobiles?
We will start by rewriting the equation. Z = [[(30)(2)
+ (1)(10)] X1 + [(30)(1.2) + (10)(1.5)] X2 + [(30)(1.1) + (10)(2.5)] X3] which is
simply
Z = [70 X1 + 51 X2 + 58 X3], so by X1, X2, X3 substation we
will have the following equations:
^
Z = [70 X1 + 51 X2 + 58 X3] - [70 X1 + 60
X2 + 58 X3]
= [70 *
0 + 51 * 411 + 58 * 1389] - [70 * 0 + 60
* 411 + 58 * 1389]
= -3699.
The
cost will fall by 3699.
What
if 1,900 auto are produced, by how much the costs will increase?
Z new =
105,222 + (60 * 1,900) = 219,222. And 219,222 - 105,222 = 114000. So the cost
will increase by 114000.
What if labor costs $35 per hour in
Bakersfield, California, what would be the new solution?
Z
= [[(30)(2) + (1)(10)] X1 + [(35)(1.5)] X2 + [(30)(1.1) + (10)(2.5) X3], which
is simply Z = [70 X1 + 67.5 X2 + 58 X3] and since the
coefficient of X2 has changed so d2 = 67.5 – 60 = 7.5, which means it increased.
In addition the Z new will be equal to [70 X1 + 67.5 X2 + 58 X3],
and by substation; Z new = [70 * 0 + 67.5 *
411 + 58 * 1389]; the final
result within the range.
Results and discussion
The first, second
and third assembly plants that Ford Company has require 2 hours, 1.5 hours and
1.1 hours of labor. Also, they require 1 hour, 1.5 hours, and 2.5 hours of machine
time to assemble one automobile. The objective function of the problem was
defined where Z is minimizing the pattern of assembly across the three
different plants. In order to make sure that we understood every single part
correctly, in every part we wrote an explanation of what we did, how did it,
and specified everything as well. The company has goal that we are trying to
achieve which is to assembling 1,800 automobiles. By solving the problem in
Excel, we got provided the solution of the problem using the previously
mentioned linear programming formulation where Z was equal to find the number
from the Excel table. At the end, we found the what-if analysis where if we
changed the production target from 1,800 to 8,000 the cost of assembling one
extra automobile will be equal to 6,200. Also, from the previous data in Figure
2 we notice that 6,200 will be out of provided range that is not acceptable.
Conclusion
In
conclusion, in the project we talked about a company called Ford that has three
different assembly plants. The assembly plants are placed in different location
all over the country with different capacity of machine times for each one of
them. We also wrote a description regarding the problem we had to find a
solution for. After that we found the linear programming formulation of the
problem and solve it using Excel Solver. We also found the sensitivity report of
the Ford Company problem and we presented a what-if analysis as well.
References
Sensitivity Analysis in Excel. (2016). Excel Easy. Retrieved 29
November 2017, from http://www.excel-easy.com/examples/sensitivity-analysis.html
The students who worked in this lab report are
- Shouq Alansari
- Hanan Akbar
- Manal Al-Mutairi
- Nour Almuwai
- Reem Almertiji
Knowing that not all students in the group have put equal efforts on this lab report. Some students worked harder than others, and it is normal when it comes to working on groups.
Things to learn from this lab report: